We discuss a number of special topics in the theory of discrete
random structures. The lecture covers both classical as well as very
recent developments. The course is structures into five themes:
- Markov chains on finite graphs, mixing time and cutoff phenomena
- Random walk and electrical networks
- Self-avoiding walk
- Percolation
- Erdös-Renyi random graphs
The aim of the course is to make students acquainted with current research topics in this area. Ideal starting point for a master thesis in this area.

- Enseignant: Markus Heydenreich
Diese Vorlesung ist eine Einführung in die Algebra. Neben den
fundamentalen algebraischen Strukturen ( Ringe, Gruppen, etc.) werden
die Grundbegriffe der Galoistheorie behandelt. Als Anwendung zeigen wir,
dass eine allgemeine Polynomgleichung von hinreichend großem Grad keine
Lösungsformel besitzt.

- Enseignant: Andreas Rosenschon
- Enseignant: Simon Weinzierl
-Diese Plattform wird ausschließlich zur Abgabe der Übungsblätter, und Erhlalt deren Korrektur verwendet.
-Ihr habt jeweils spätestens bis Donnerstags um 10:15 Uhr Zeit eure Lösungen als "PDF Dokument" hochzuladen.
-Gruppenarbeit ist zugelassen. Bei einer Gruppenarbeit reicht es aus wenn nur ein Person die Lösungen im Namen der Gruppe hochlädt, allerdings die Namen von allen Gruppenmitglieder sollten im Dateinamen des PDF-Dokumentes erwähnt sein.
-Die Übungsblätter werden Wochenlicht in der Kurswebseite veröffentlicht.
- Enseignant: Sahand Tokasi
Tentative Agenda
1) Numerical Methods and Computational Finance
- Algorithmic Differentiation / Adjoint Algorithmic Differentiation
- Stochastic Algorithmic Differentiation
- Monte-Carlo Simulation on GPUs (NVIDIA Cuda and OpenCL)
2) Hybrid Market Models, Complex Derivatives and their Object-Oriented Implementation
- Foundations in mathematical finance and their implementation (stochastic processes)
- Interest Rate Models
- Hybrid Market Models (Cross-Currency Modeling, Equity Hybrid Model, Defaultable LIBOR Market Model) and their object oriented implementation
- Definition of model interfaces
- The valuation of complex derivatives
- Model calibration
- Special topics from risk management
The lecture covers the object oriented implementation of the algorithms in Java and using modern software development tools.
As part of the implementation of the models and the valuation algorithms, the lecture will discuss some of the latest standards in software development.
- revision control systems (Git)
- unit-testing (jUnit)
- build management (Maven, Gradle)
- continuous integration (TravisCI, Jenkins)
Implementation will be performed in Java (Eclipse, IntelliJ)

- Enseignant: Roland Bachl
- Enseignant: Christian Fries
- Enseignant: Andrea Mazzon
- Enseignant: Lukas Gonon
- Enseignant: Thomas Reitsam
A Lie group is a group which is also a smooth manifold, in way that the group multiplication and the inversion are smooth maps. Examples of Lie groups are matrix groups like the linear group GL(n,R) or the orthogonal group O(n). Lie groups play an important role in many parts of mathematics and physics. They almost inevitably occur when a problem or configuration is invariant under symmetries.
In the lecture we will discuss structural results about Lie groups as well as examples and applications. An important tool will be the Lie functor, which assigns to every Lie group its so-called Lie algebra. The Lie algebra is an infinitesimal version of the Lie group that encodes surprisingly much information about it, and that can be well studied via methods from linear algebra. This will allow us to establish a classification of complex semi-simple Lie algebras and of compact Lie groups. In doing so we will argue from a geometric perspective whenever possible. In particular, we will follow an approach suggested by Cartan that is more geometric than the standard one.
- Enseignant: Christian Lange
Das Einschreiben in diesen Kurs ist ab Donnerstag den 29. Oktober 2020 möglich um 10 Uhr möglich. Den Einschreibeschlüssel finden Sie auf folgender Webseite: http://www.math.lmu.de/~hofer/linalg1/main.php
- Enseignant: Werner Bley
- Enseignant: Martin Hofer
- Enseignant: Sohir Maskey
- Enseignant: Pascal Stucky
- Enseignant: Dirk Deckert
- Enseignant: Markus Nöth
- Enseignant: Simon Reisser
- Enseignant: Konstantinos Panagiotou
- Enseignant: Aaron Söhnen
- Enseignant: Niklas Walter
- Enseignant: Thomas Beekenkamp
- Enseignant: Annika Heckel
- Enseignant: Noela Müller
- Enseignant: Konstantinos Panagiotou
- Enseignant: Simon Reisser
- Enseignant: Alejandro Caicedo
- Enseignant: David Geldbach
- Enseignant: Sabine Jansen
- Enseignant: Stefan Wagner
We give a brief introduction to the K-theory of rings and schemes and then focus on various aspects of the K-theory of curves.
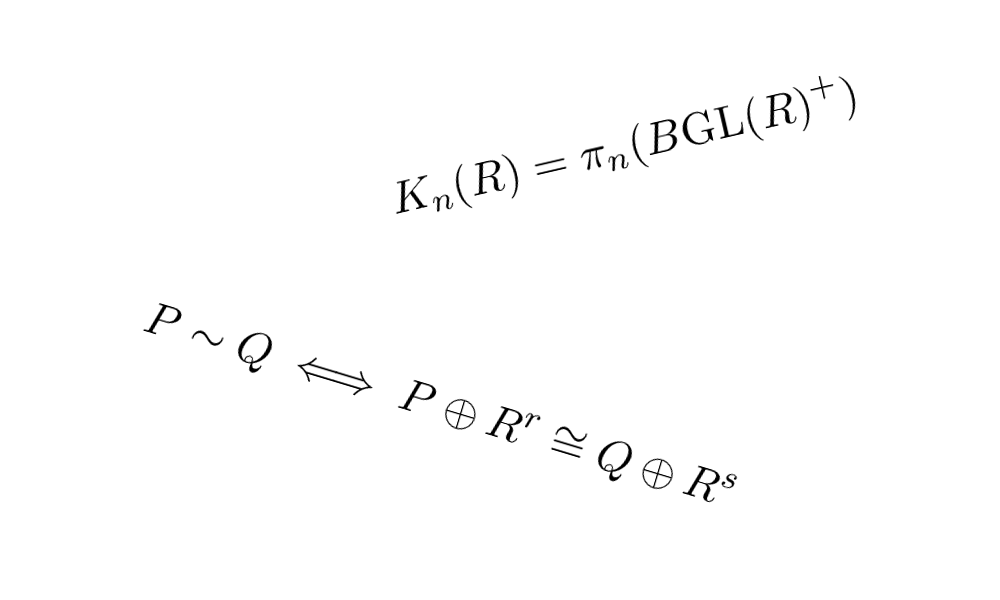
- Enseignant: Andreas Rosenschon
- Enseignant: Simon Weinzierl
- Dozent: Dieter Kotschick
- Dozent: Jonas Stelzig